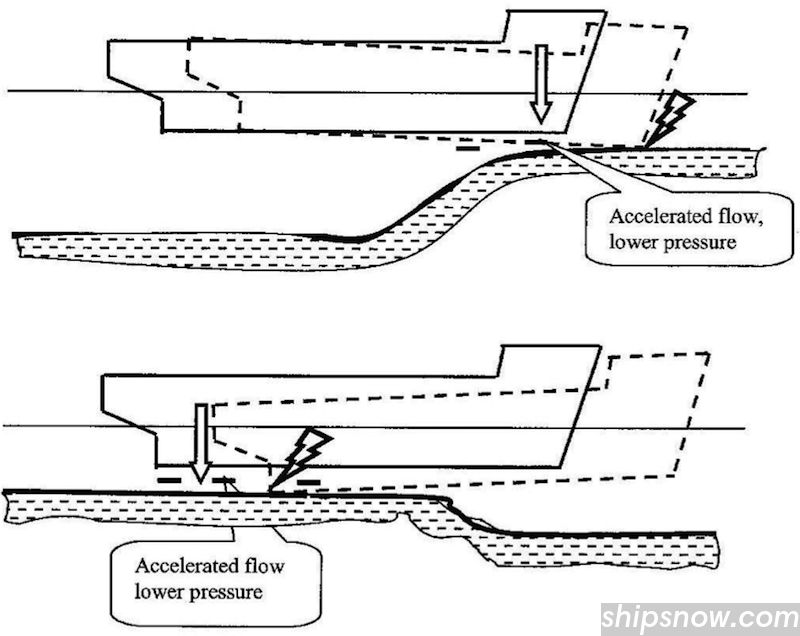
Interaction Effects

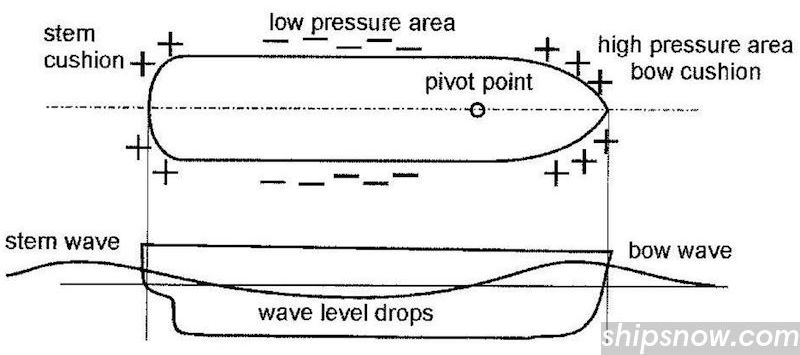
Pressure distribution around ship hull.

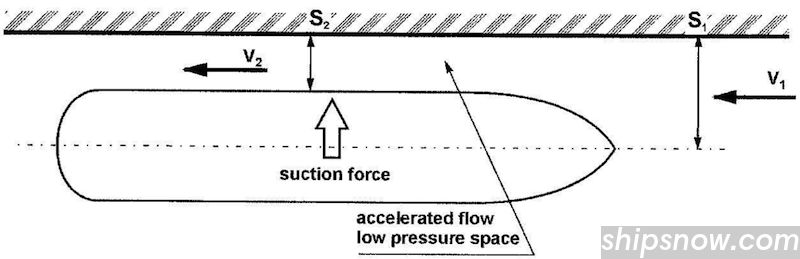
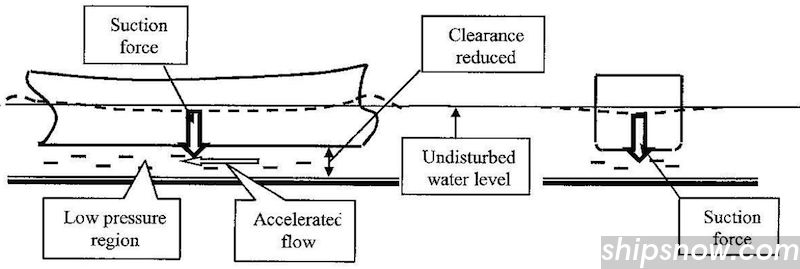
Wall Effect – Suction Force

When the ship is moving close to a solid wall or bank then there is a reduction of the flow cross section area between the ship and the bank (from S1 to S2).

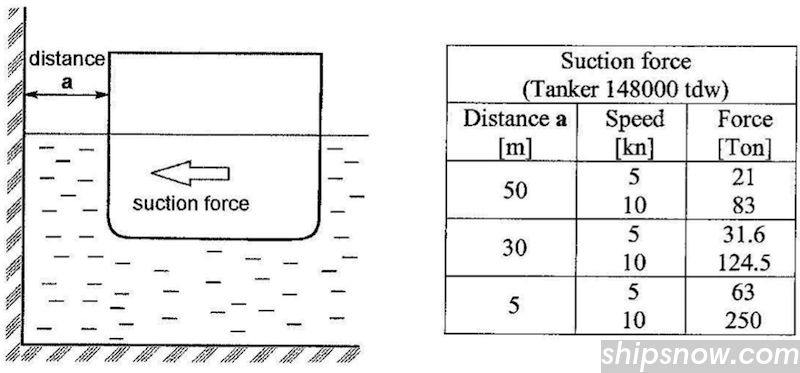
The suction force is proportional to the speed of the ship squared and inversely proportional to the distance from the bank. Suction forces calculated for an example ship are shown below.

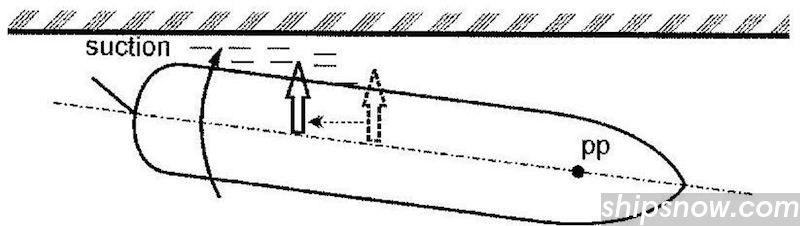
Using Suction Force to the Advantage

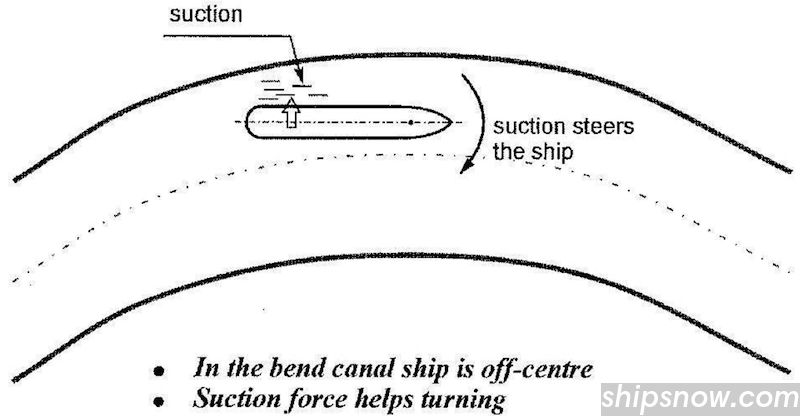
Passing Through a Narrow Passage

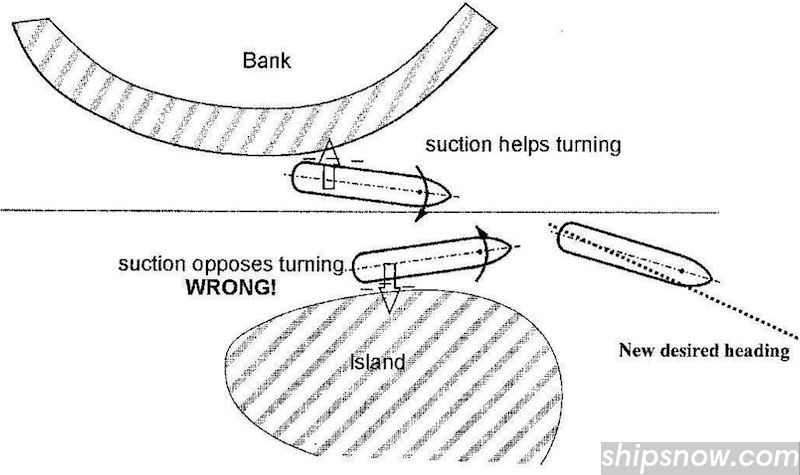
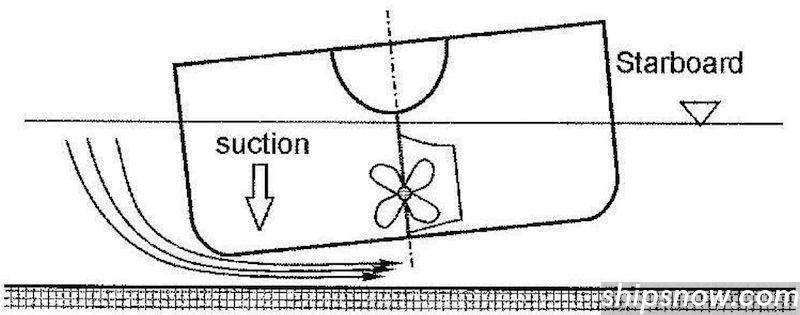
Entering the passage closer to the port side bank the suction force helps turning to starboard as needed.

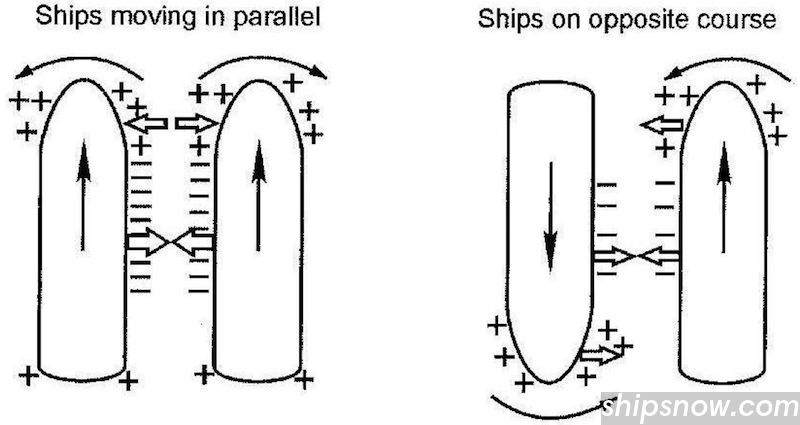
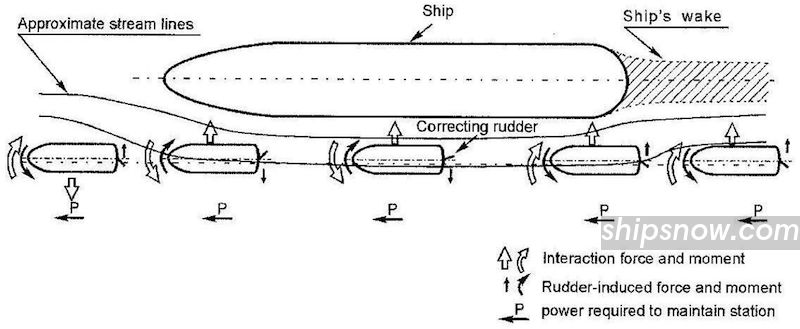
Interaction Effects Between Two Ships

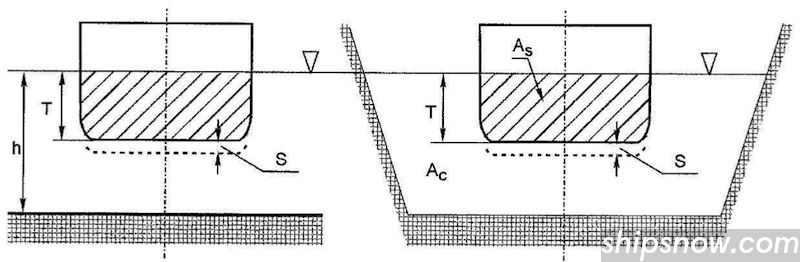
Squat

Formulas for Squat Assessment

There is a number of different formulas for squat calculations. The simplest formulas are formulas proposed by Barrass (see below).

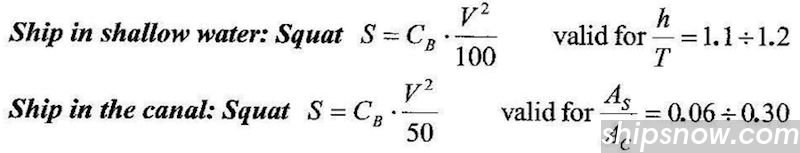
Effect of Heeling on Squat

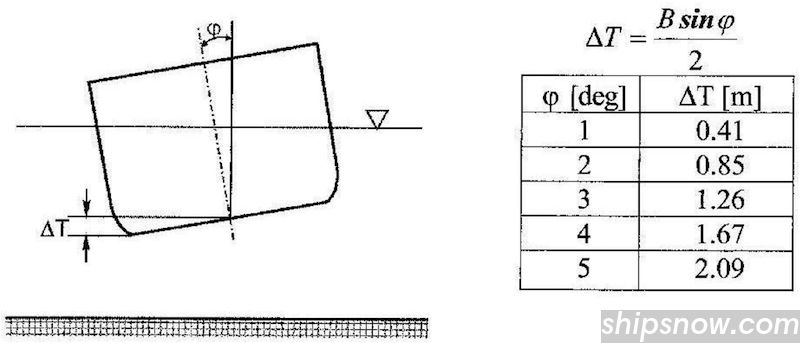
Sinkage When Turning

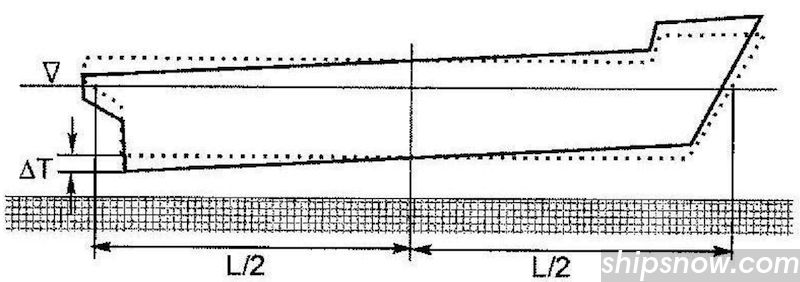
Effect of Trim

Entering or Leaving Shalow Bank